初中时我们都学过勾股定理
a2 + b2 = c2
当时完全是死记硬背的。
五一后的周六(2021-05-08),鑫哥说到他儿子学习的课程知识点“等差数列”。 他问:1+3+5+7+9+...+N等于多少?
答案是(1+N)*个数/2。
算法(其一)如下:
S1=1+3+5+7+9+...+N
S2=N+(N-2)+(N-4)+(N-6)+...+1
可知S1和S2相等。再把如上两个等式的左右分别相加。即
S1+S2 = (1+N)*个数
2*S1 = (1+N)*个数
即S1=(1+N)*个数/2,即是结果。
注意~~,上面是数学解法。
后来又聊到这个题其实有几何解法。就是借助梯形,把上面的题想像成求梯形的面积(梯形的面积=(上底+下底)*高/2)试试。
接着我就推荐了之前看到的一个视频读了这本书,你会喜欢上数学么?《万物皆数》,里面说使用几何来解释数学公式。
接下来我和另一个同事就玩起来了。想用几何证明
(a+b)2 = a2 + b2 + 2*a*b
(a-b)2 = a2 + b2 + 2*a*b
a2 = (a-1)2 + (a+1)2 + 1
a2 + b2 = c2
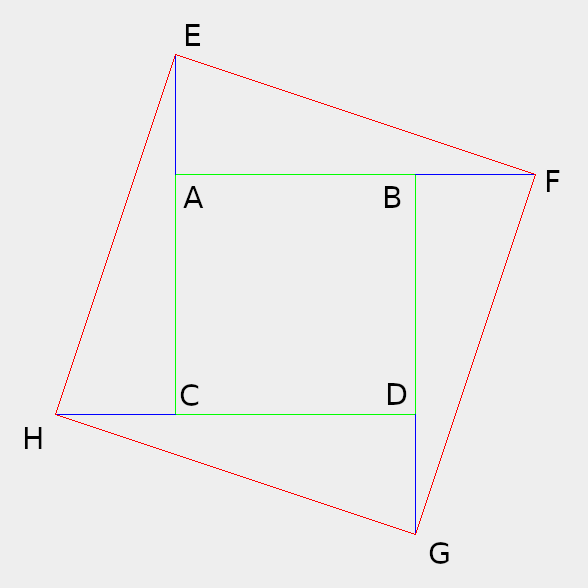
今天我就先把最后一个证明的过程记录下来。其实当天我就想写本篇博客,但当时我使用GIMP画不出下面的图形,就拖了几天。今天(2021-05-14)下班前又打开GIMP画图,灵机一动,我为什么要用软件画呢,我用程序画啊…… 半小时后程序界面如下(A~H点是使用GIMP画上的)
我们想证明a2 + b2 = c2,由上图可知
先接受一个前提:一个数a的平方用几何解释就是边长为a的正方形的面积。
如下是证明过程:
a = EA, b, = AF, c = EF
要证明的即是
EA2 + AF2 = EF2
反过来就是
EF2 = EA2 + AF2
边长为EF的正方形的面积 = 中间的小正方形的面积 + 4个外部直角三角形的面积,即
EF2 = (AF-BF)2 + EA*AF/2*4
展开就是
EF2 = AF2 + BF2 - AF*BF*2 + EA*AF/2*4
由图中可知EA=BF,将所有的BF换成EA,即
EF2 = AF2 + EA2 - AF*EA*2 + EA*AF*2
最后两项消去,即
EF2 = AF2 + EA2
结束。
备注:
- 以后要花时间看看上面视频中说到的《万物皆数》。
- 上面解题的前置条件是完全平方公式的展开,(其实它也有几何解法,并且还比较简单~~)
EA2 = (AF-BF)2 = AF2 + BF2 - AF*BF*2
-
如上思索过程并没有上网查资料。
-
附上程序代码:
import java.awt.*;
import javax.swing.*;
/**
* 用几何验证数学公式-勾股定理.
*
* 勾股定理 a2 + b2 = c2
*/
public class A2PlusB2EqC2 extends JPanel {
/** 总面板的宽和高,宽高一样,很方便 */
private static final int WIDTH = 600;
private static final int HEIGHT = 600;
/** 每个小方格的宽/高 */
private static final int GRID = WIDTH / 10;
/**
* 如下是A点~H点,先在纸上画出比较好,草图即是上面的图
*/
private static final Point POINT_A = new Point(GRID * 3, GRID * 3);
private static final Point POINT_B = new Point(POINT_A.x + GRID * 4, POINT_A.y);
private static final Point POINT_C = new Point(POINT_A.x, POINT_A.y + GRID * 4);
private static final Point POINT_D = new Point(POINT_B.x, POINT_C.y);
private static final Point POINT_E = new Point(POINT_A.x, POINT_A.y - GRID*2);
private static final Point POINT_F = new Point(POINT_B.x + GRID*2, POINT_B.y);
private static final Point POINT_G = new Point(POINT_D.x, POINT_D.y + GRID*2);
private static final Point POINT_H = new Point(POINT_C.x - GRID*2, POINT_C.y);
public A2PlusB2EqC2() {
setPreferredSize(new Dimension(WIDTH, HEIGHT));
}
@Override
public void paint(Graphics g) {
super.paint(g);
g.setColor(Color.GREEN);
g.drawRect(POINT_A.x, POINT_A.y, POINT_D.x - POINT_C.x, POINT_D.y - POINT_B.y);
g.setColor(Color.BLUE);
linePoint(g, POINT_A, POINT_E);
linePoint(g, POINT_B, POINT_F);
linePoint(g, POINT_D, POINT_G);
linePoint(g, POINT_C, POINT_H);
g.setColor(Color.RED);
linePoint(g, POINT_E, POINT_F);
linePoint(g, POINT_F, POINT_G);
linePoint(g, POINT_G, POINT_H);
linePoint(g, POINT_H, POINT_E);
}
private void linePoint(Graphics g, Point p1, Point p2) {
g.drawLine(p1.x, p1.y, p2.x, p2.y);
}
public static void main(String[] args) {
JFrame frame = new JFrame();
frame.setContentPane(new A2PlusB2EqC2());
frame.setTitle("用几何验证数学公式-勾股定理");
frame.setLocation(500, 100);
frame.setDefaultCloseOperation(WindowConstants.EXIT_ON_CLOSE);
frame.setVisible(true);
frame.pack();
}
}